mathworld.wolfram.com/Derivative.html
lunes, 13 de noviembre de 2017
domingo, 12 de noviembre de 2017
Razón de cambio
=RAZÓN DE CAMBIO=
Razón de cambio (de una variable respecto a otra) es la
magnitud del cambio de una variable por unidad de cambio de la otra. (También
se le llama tasa de cambio.) Si las variables no tienen ninguna dependencia la
tasa de cambio es cero.
En general, en una relación funcional y=f(x), la razón de cambio de
la variable dependiente y
respecto a la independiente x
se calcula mediante un proceso de límite:
De la razón [ f
( x
+ t )
− f (
x )
] / t
Denominada cociente diferencial.
La razón de cambio es el límite del cociente diferencial
cuando t
tiende a cero. De esta manera, la razón de cambio es la interpretación
fundamental de la derivada de una función.
La derivada como razón de cambio maneja dos tipos de razón
de cambio, en estas se ven muchos problemas relacionados y con una solución muy
larga:
-
Promedio: Se trata de problemas en los que
estudiamos fenómenos relacionados con la variación de una magnitud que depende
de otra.
-
Instantánea: Se le denomina segunda derivada y
hace referencia a la velocidad con la cual cambia la pendiente de una curva en
un momento determinado.
Máximos y mínimos
Valores máximos y mínimos de una función |
|||||
En dos puntos se presentan tangentes
horizontales; y es justo en aquellos en donde la función cambia de ser
creciente a decreciente o viceversa.
|
|||||
 |
|||||
Un máximo o mínimo absoluto se
refiere al valor mayor o menor que puede tomar una función en TODO su
rango. En el ejemplo que ilustramos, el máximo absoluto es el infinito y
sucede cuando x toma valores infinitos también. El mínimo absoluto está en
menos infinito y ocurre cuando x se acerca a menos infinito también.
|
|||||
Un máximo o mínimo relativo se
refiere al valor mayor o menor que toma una función en un determinado
intervalo. En el ejemplo, la función tiene un valor máximo aparentemente en el punto (-2, 3) y un mínimo aparentemente en (-1, 0).
 |
|||||
2) f(x) = x3 − 3x + 2
|
f'(x) = 3x2 − 3 = 0 x = − 1 x = 1
Candidatos a extremos: − 1 y 1.
f''(x) = 6x
f''(−1) = −6 < 0 Máximo
f''(1) = 6 > 0 Mínimo
f(−1) = (−1)3 − 3(−1) + 2 = 4
f(1) = (1)3 − 3(1) + 2 = 0
Máximo(−1, 4) Mínimo(1, 0)
2)
Candidatos a extremos: − 1 y 1.
f"( − 1) = 6 > 0 Mínimo
f"(1) = − 6 < 0 Máximo
f(−1) = 3 · (−1) − (−1)³ = − 2
f(1) = 3 · 1 − 1³ = 2
Máximo ( − 1, − 2) Mínimo(1,
2)
Derivadas de orden superior
Derivadas de Orden Superior
La derivada de orden superior se conoce como la segunda, tercera,
etc derivada de la función, es decir, si f(x) es una función y existe su
primera derivada f´(x). A tener en cuenta:
es la derivada de
la función 
es la derivada de
la derivada de la función
Notación de la Derivada de Segundo
Orden
Existen otras formas de expresar la
derivada de segundo orden:
Derivadas de funciones implícitas
Derivadas de funciones implícitas
Funciones implícitas
|
||||||||||
Las funciones pueden clasificarse en
funciones explícitas e implícitas. Una función en la que la variable
dependiente se expresa ÚNICAMENTE en términos de la variable independiente es
una función explícita. La forma de estas funciones es y = f(x), y al
derivarlas, la idea es encontrar y’. Por ejemplo, la función
 es una función explícita. |
||||||||||
En los casos en los que nuestra
variable dependiente no esté expresada sólo en términos de la variable
independiente, se tiene una función implícita. Una expresión equivalente
a
es . Esta expresión no nos presenta a
y en términos de x, por lo que en este caso tenemos a la función definida de
manera implícita. 
Derivación de funciones implícitas
Aplicando las fórmulas de derivación a la
expresión,
 tenemos:
2x+2yy´=0
2yy´=-2x
Y´=-2x/2y
Y´=-x/y
|
||||||||||
. Derivar esta expresión, tal y
como sucedió antes, implica derivar ambas partes de la igualdad. Esto
es
.
o 
Derivadas de funciones exponenciales y logarítmicas
Derivadas de funciones exponenciales y
logarítmicas.
Se aplican los mismos conceptos, pero teniendo como
base a las fórmulas 11 a 14 y 27.
Derivadas de funciones inversas
Derivadas de funciones inversas.
Aplicamos los mismos conceptos anteriores, teniendo
ahora como base las fórmulas 21 a 26.
Por ejemplo:
Derivadas de funciones trignométricas
Derivadas de funciones trigonométricas
Para este tipo de derivada, utilizaremos como base
las formulas 15 a 20, aplicando los mismos conceptos anteriores. A veces nos
podemos ahorrar bastante trabajo si buscamos simplificar la expresión antes de
derivarla.
Por ejemplo:
F(x) = Sen8x
F´(x) = 8 cos8x Se aplicó la fórmula 15, a manera
de multiplicar la derivada de seno (coseno) por la derivada del ángulo 8x.
Ó
Derivadas por fórmulas
Derivadas por fórmulas.
Para este tipo de ejercicios, aplicaremos las Formulas para
derivar de manera directa. Por ejemplo:
Derivada de una
constante
f(x) = k f´(x) = 0
Derivada de x
f(x) = x f´(x) = 1
Luego nos podemos enfrentar a planteamientos donde
se deben aplicar varias de estas fórmulas al haber más de una involucrada.
Por ejemplo:
F(x) = 7x3 – 3x2 + 3x -12
Tenemos cuatro distintos términos para derivar, al estar separados por signos.
F´(x) = (7)(3) x2 – (3)(2) x + 3 – 0 Aplicando
la fórmula 6 en los tres primeros términos, y la fórmula 1 en el último.
F´(x) = 21x2 – 6x + 3 Para, por último,
simplificar.
Ó
Fórmulas para derivar
Estas son las 27 principales fórmulas que utilizaremos para determinar las
derivadas.
Derivar por definición
Derivar por definición
Para derivar por definición,
se utiliza la REGLA DE LOS CUATRO PASOS.
El procedimiento en este caso consiste en los pasos
siguientes:
- 1. Se da un incremento, Dx a la variable independiente x
- 2. Se obtiene el incremento correspondiente a la función
- 3.- Se obtiene el cociente de los incrementos
- 4.-Se calcula el límite del cociente de incrementos y esto proporciona la derivada de f (x)
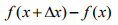
Derivada
Derivada
La derivada de una función representa un cambio
infinitesimal en la función con respecto a una de sus variables. Mide la
rapidez con la que cambia el valor de dicha función matemática, según cambie el
valor de su variable independiente. Está representada gráficamente como una línea recta superpuesta sobre cualquier curva (función).
Debemos encontrar el valor de la pendiente de la recta
tangente.
Sustituimos las
denominaciones en la fórmula original de la pendiente.
Esto lo podemos simplificar aún más, a manera de formar un triángulo rectángulo, donde el cateto de abajo nos dice la variación que hay entre las dos “x”.
El punto (X2,
Y2) cada vez se aproxima más al punto (X1, Y1),
pero sin llegar a tocarlo, es decir, el incremento de X va disminuyendo, en
otras palabras, va tendiendo a 0.
Así que, al aplicar la teoría sobre limites matemáticos,
resulta la siguiente expresión:
Para
terminar, recordemos que
Por lo tanto
Y queda:
Lo que viene siendo la "Derivada"
LÍMITES DE FXS TRIGONOMÉTRICAS INDERTERMINADAS
Ejemplo de Límites Trigonométricos Indeterminados
0/0
Resolver
1.
Circunferencia unitaria y figuras geométricas
Circunferencia Unitaria
Tal y como su nombre lo indica en la circunferencia unitaria el radio es igual a uno (r = 1), y por conveniencia el centro se considerará en el origen de los ejes coordenados O(0,0).
Utilizando la fórmula de la distancia entre dos puntos se obtiene la ecuación que define a una circunferencia con radio igual a uno:
Localizar puntos. Los ejes coordenados dividen a la circunferencia en cuatro partes iguales (1/4) por lo que la medida del arco de la circunferencia en cada cuadrante es igual a p / 2. La longitud de la circunferencia está dada por la siguiente fórmula:
Por 1/4 de vuelta tenemos:
Para localizar un punto cualquiera en la circunferencia unitaria se parte siempre del primer cuadrante; si el punto es positivo el desplazamiento es en sentido inverso a las manecillas del reloj; si el punto es negativo entonces el desplazamiento es en el sentido de las manecillas del reloj.
El punto P(2) se localiza en el segundo cuadrante porque:
p = 3.14 y p / 2 = 1.57 y como 1.57 < 3.14 P(2) es un punto en el segundo cuadrante porque 2 - 1.57 = 0.43
Identidades Trigonométricas
Son igualdades que se satisfacen para cualesquiera valores de las variables, excepto para aquellos que no tengan sentido. Las identidades trigonométricas se clasifican en:
Pitagóricas
De cocientes
De recíprocos
Triángulo Rectángulo
Se caracterizan porque uno de sus tres ángulos es de 90°, y por definición la suma de los ángulos interiores de un triángulo es de 180°. Por lo que, un triángulo rectángulo puede resolverse cuando se conocen:
1. Los tres lados
2. Dos lados y el ángulo comprendido entre ellos
3. Dos ángulos y un lado.
4. Dos lados y el ángulo opuesto a uno de ellos
Valores de las Funciones Circulares para Arcos p / 4, p / 6, p / 3
Se calcularán las coordenadas del punto terminal de un arco de longitud p / 4. Se traza una circunferencia unitaria y se localiza el punto en dicha circunferencia:
Si p = 3.14 entonces p / 4 = 3.14 / 4 = 0.785 en radianes ó 180° / 4 = 45° en grados
Se trazan segmentos de recta perpendiculares a ambos ejes pasando por el punto P( p / 4)
Unimos el origen O(0, 0) con el punto para obtener un triángulo por construcción geométrica
Las coordenadas del punto y sus múltiplos serán
Se calcularán las coordenadas del punto terminal de un arco de longitud p / 3. Se traza una circunferencia unitaria y se localiza el punto en dicha circunferencia:
Si p = 3.14 entonces p / 3 = 3.14 / 3 = 1.046 en radianes ó 180° / 3 = 60° en grados
En una circunferencia unitaria cuyo centro coincide con el origen del sistema de coordenadas rectangulares, se traza una cuerda AB de longitud igual a la unidad:
A partir de B, se traza otra longitud unitaria BC. Desde C otra cuerda CD y se continúa con las cuerdas contiguas de longitud unitaria DE, EF y FA:
Se construye un hexágono regular con lados de longitud igual a uno (1), en consecuencia AB es la sexta parte de la distancia que se mide alrededor de la circunferencia, esto es:
De esta manera se obtiene un triángulo equilátero OA = OB = AB = 1 Por geometría OH = 1/2 y aplicando el Teorema de Pitágoras se tiene:
Las coordenadas del punto y sus múltiplos serán
Se calcularán las coordenadas del punto terminal de un arco de longitud p / 6. Se traza una circunferencia unitaria y se localiza el punto en dicha circunferencia:
Si p = 3.14 entonces p / 6 = 3.14 / 6 = 0.523 en radianes ó 180° / 6 = 30° en grados
Por construcción geométrica y = 1/2 se obtiene un triángulo
Utilizando el Teorema de Pitágoras se tiene:
Las coordenadas del punto y sus múltiplos serán
Suscribirse a:
Entradas (Atom)